Cross Breeder Editor

Applies to:FA 5

The Cross Breeder editor allows you to combine 2 fractal keyframes (those fractals may be layered multi-fractals).

You might have hundreds of potential layer/transform morph combinations from just a pair of keyframe fractals.

Cross Breeder Panels

A. Cross Breeding Result Thumbnail
B. KeyFrames and Breeding Amount Slider
C. Cross Breeding Interpolation Controls
D. Interpolation Curve Controls
E. High Quality Video Controls

Cross Breeder Window Sections

KeyFrames & Breeding Amount Slider

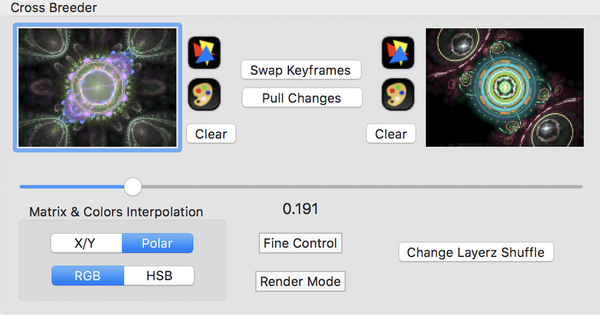
Left & Right Keyframes

Use either drag & drop or cut & paste to setup the keyframes.
You can choose any thumbnail from elsewhere in the application or select a Flame file from the Mac Finder to populate a keyframe.

You can open the Triangle editor or the Color Gradient and make changes to the keyframes. After editing them, make sure you click the Pull Changes button so the Cross-breeder gets the changed keyframes.

Keyframe Buttons

Swap Keyframes: Swaps the keyframes.
Open Transform Editor: Modify the keyframe with the Transform editor.
Open Color Gradient Editor: Modify the keyframe’s color palette.
Pull Changes: After editing the keyframes, this button pulls their current state into the CrossBreeder.
Clear: Removes the keyframe.

Cross Breeding Amount Slider

The slider controls the amount of the morph between the two keyframe fractals.

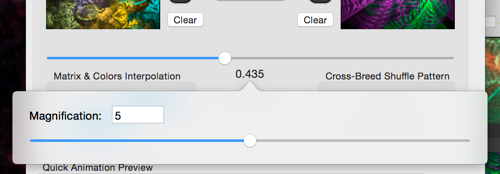
If you click the Fine Control button, a popup window with another slider appears. You can adjust the effective magnification amount control slider. Larger number gives you finer control over the affect of the slider’s movement.

Transformation Matrix and Color Interpolation Options

These change the way interpolation is done to the transforms’ matrices and to the color values.

X/Y <==> Polar: Interpolate X/Y matrix coordinate values or interpolate polar matrix coordinate values.
RGB <==> HSB: Interpolate either Red-Green-Blue color values OR interpolate Hue-Saturation-Brightness color values.

Render Mode

The Render Mode button allows you to apply image compositing and transparency effects on the output.

See: Render Mode

3D Camera Orientation Interpolation

Morphing of 3D Camera pitch, yaw, and roll are now done using Spherical Linear Interpolation - so you now have better smooth changes in camera orientation from a morph.

Cross-Breed Shuffle Patterns

A morph takes the transforms from fractal 1 and transform from fractal 2 and blends them together.

The shuffle permutations are just different arrangements of which transform of fractal1 is blended with which transform of fractal2.

Here the permutation is 1, 2, 3:

Flame 1		Flame 2
Xform 1	===>	Xform 1
Xform 2	===>	Xform 2
Xform 3	===>	Xform 3

But there are other combinations. For example:

Here the permutation is 2, 3, 1.

Flame 1		Flame 2
Xform 1	===>	Xform 2
Xform 2	===>	Xform 3
Xform 3	===>	Xform 1

With 3 transforms, there are 6 different shuffle permutations.

The number of permutations for n transforms is: n! or n factorial.

n factorial is defined to be: n * (n - 1) * (n - 2) … 2, 1

So:

if n = 3, n! = 3 * 2 * 1 = 6

if n = 4, n! = 4 * 3 * 2 * 1 = 24

With the these two fractals each have 6 transforms to be morphed together. There are 720 different shuffle combinations where the right transform can be morphed with a transform on the left. The number of combinations is n factorial (6! = 720). If there are only

You will get a different morph animation with each shuffle combination. So in this example, you get 720 different morph animations from just 2 keyframes!

The default shuffle pattern is for the 1st left transform to be morphed to the 1st on the right, 2nd left to 2nd right, …

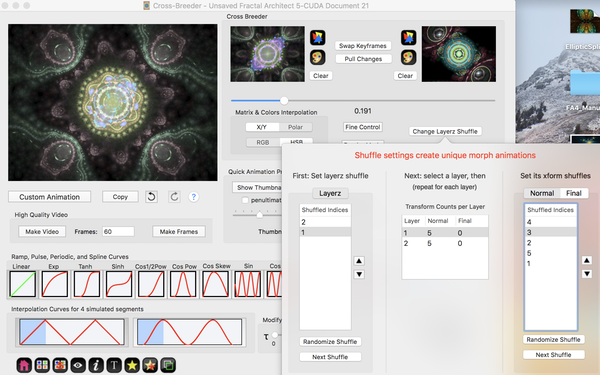
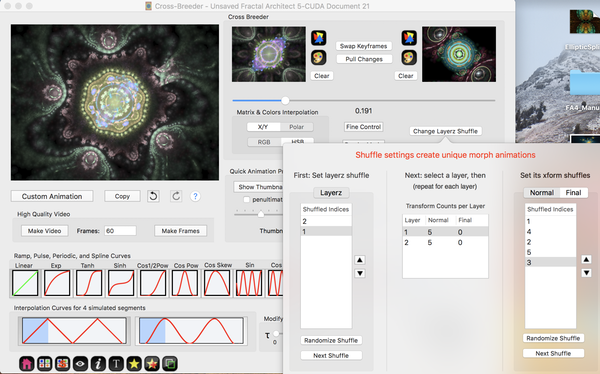
Layerz Permutation

Just like with transforms, when a fractal has more than one layer, you also have many layer permutations.

Layerz Permutations - How to Use

Set layerz shuffle first.
Then for each selected layer (select it on the left), set its transform shuffle.
Since fractals can have multiple final transforms, remember to set this shuffle too.

How to Edit a Shuffle

First, set the crossbreeding amount slider close to 0.5. That way you can see middle of the animation.
These are the ways:

Manually by selecting a shuffle index and moving it up or down the table, by pressing the Up and Down arrow buttons next to the table.
Click the Randomize Shuffle button.
Click the Next Shuffle button.

Same Keyframes - Many Crossbreeder Permutations

The fractal shown here has 2 layers, each layer has 5 normal transforms and 0 final transforms. For this example, there are 240 different permutations available.

Picking a Permutation

Pick a layer shuffle first, then select a nice xform shuffle. Set the morph amount slider somewhere in the middle of its range. (At the endpoints, you will only see the original keyframes !)

Showing Interpolated Thumbnails

You can show a number of thumbnail images with different interpolated values.

Interpolated result

Opening the Interpolator

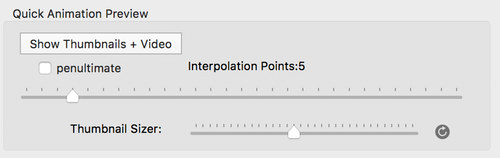
First, set the Interpolation Points to the desired number of thumbnails images to show.
Next click on the Show Thumbnails button.

Tip: You can first open it with a small number of points to see if the parameter has much affect on the image.
If it does, you may reopen it a second time with more thumbnails.

Adjusting the Thumbnails’ Size

Use the sizing slider to select a new size, then press the redraw button.

Setting the parameter’s value to one of the interpolated values.

Below each image the actual parameter’s value is shown in red.
Click the desired thumbnail image with the mouse to select it.
Press the Return key to set the parameter’s value. Or double-click on the image to set the parameter’s value.
The interpolator window will close.

Showing a Video of the Interpolated Results

First, set the Interpolation Points to the desired number of thumbnails images to show.
Next click on the Show Thumbnails & Video button. Finally click on the Show Video button. In a moment a video containing the interpolated thumbnail images will be shown.

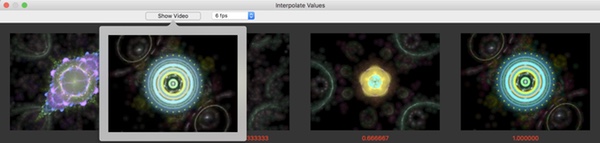
Thumbnail Image’s Context Menu

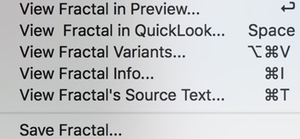
Opening a new Preview window with contents of a specific thumbnail

Click the thumbnail image with the mouse to select it.
Press the Return to open the Preview window or use the the right mouse button activated context menu to open it.

Showing the Quicklook view for a specific thumbnail

Click the thumbnail image with the mouse to select it.
Press the spacebar to open the Quicklook view or use the the right mouse button activated context menu to open it.

Opening the Variants editor for a specific thumbnail

Click the thumbnail image with the mouse to select it.
Use the the right mouse button activated context menu to open it.

Saving the thumbnail’s fractal definition to a new file

Click on the thumbnail image to select it. Next right click on the thumbnail and select the “Save Selected Frame’s Fractal” menu item.

Interpolation Curve Controls

Whats a Ramp, Pulse, or Periodic Curve?

Ramp

Curve starts at the right keyframe and ends at the left keyframe.

Pulse

Curve starts at the right keyframe goes to the left keyframe, and then returns to right keyframe.

Periodic

Curve cycles back and forth between the keyframes.

Interpolation Curve Types

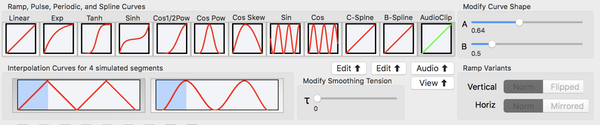
Curves affect the interpolated parameter values. The default Linear Ramp curve interpolates linearly from start to end parameter values.

The bottom of the curve box represents the left keyframe flame fractal. The top represents the right keyframe flame fractal.

Linear Ramp (default)

Not effected by A or B curve shape parameters.

Exponential Ramp

Affected by just A curve shape parameter.

Tanh Ramp

Affected by just A curve shape parameter.

Sinh Ramp

Affected by just A curve shape parameter.

Cos Half-Power Ramp

Affected by just A curve shape parameter.

Cos Power Pulse

Affected by just A curve shape parameter.

Skewed Cos Power Pulse

Affected by both A and B curve shape parameters.

Sin Periodic

Affected by both A and B curve shape parameters.

Cos Periodic

Affected by both A and B curve shape parameters.

Catmull 2D Spline

Use the Edit button to open the curve editor.

B-Spline 2D

Use the Edit button to open the curve editor.

Audio Clip

Use the Audio button to use a audio sound clip to create a curve.

Smoothing Types

The affect of the Smoothing over 4 concatenated animation segments is shown in the graphic.

None

No smoothing is applied.

Smooth

Catmull-Rom spline smoothing. Tension (tau) parameter applies.

Ramp Variants

You can flip a curve upside-down or mirror it horizontally. This can be used to reverse the animation.

Norm

No change to animation order.

Flipped

Curve is flipped upside-down.

Mirrored

Curve is mirrored horizontally.

Catmull 2D Spline Editor

This curve editor allows you to create your own custom curve for the morph amount.

Catmull curves first and last control points (the green points) do not lie on the curve, but still influence the curve’s shape.

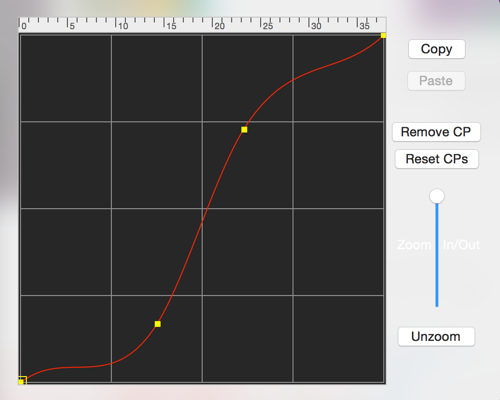
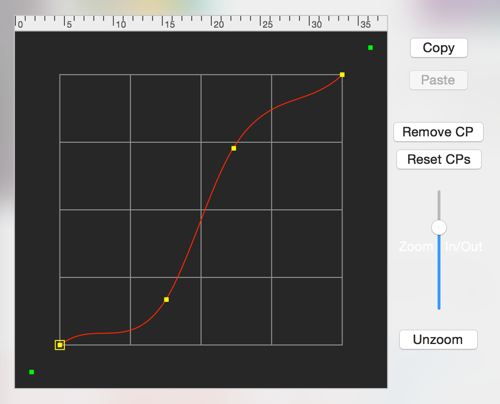
Mouse Click and Drag

Click on the red line with the mouse to add a new point and then drag it to shape the curve. If you click on top of an existing point, that point will be selected and can be dragged to shape the curve.

The first and last control points are hidden and can be revealed by zooming out the curve editor. They are the green points. The 2nd and next-to-last points in the curve can only be dragged along the X and Y axes of the graph.

Copy: Copy the curve to the clipboard.
Paste: Paste a curve from the clipboard.
Remove CP: Remove the selected control point. The first 2 and last 2 control points cannot be removed.
Reset CPs: Reset the control points to the default linear curve.
Zoom Slider: Zoom the curve display in or out (so you can see the first and last control points.)
Unzoom: Unzoom back to the default zoom level. Hides the first and last control points.

B-Spline 2D Spline Editor

This curve editors allows you to create your own custom curve for the morph amount.

B-splines are a free from curve that tends to have smoother curves than Catmull curves.

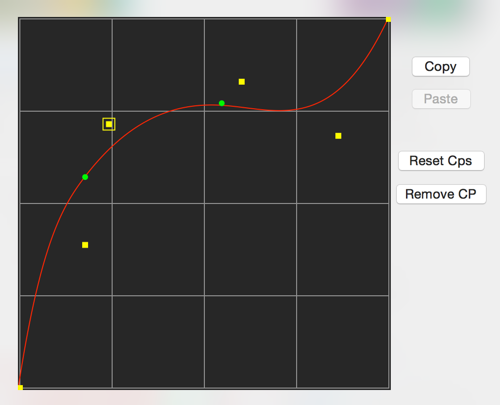
Mouse Click and Drag

Click on the graph with the mouse to add a new point and then drag it to shape the curve. If you click on top of an existing point, that point will be selected and can be dragged to shape the curve.

With B-splines, only the first and last control points lie on the curve. The rest help shape the curve.

The first and last points in the curve can only be dragged along the X and Y axes of the graph. Unlike the Catmull curve editor, there is no zoom control as there are no hidden control points.

Copy: Copy the curve to the clipboard.
Paste: Paste a curve from the clipboard.
Remove CP: Remove the selected control point. The first 2 and last 2 control points cannot be removed.
Reset CPs: Reset the control points to the default linear curve.